Pythonの実践的な練習として、リバーシゲームの作成をしてみましょう。
ソースはこちらからダウンロードできます。
この記事を読むことで、以下のことが身に付きます!
- ソフトウェア設計の基礎が分かるようになる。
- リバーシの実装をできるようになる。
- MVCモデルについて理解することができる。
- 数百行程度の量のコーディングができるようになる。
MVCモデルとは、ソフトウェアアーキテクチャの一種で、「こういう風にソフトウェアを作るとうまくいくよ」というものです。
MVC?アーキテクチャ?なにそれおいしいの、という人は、リバーシくらいなら設計うんぬん考えずに、がーっと1つのソースコードに書いてしまう方が楽で良いと思うかもしれません(がーっと書くのも良い練習になりますがそれは置いておいて)。MVCモデルを用いるメリットは、以下があります。
- 複雑になりがちなUIの実装を分かりやすく書くことができる。
- モジュール結合度が弱くなる。
(どれか1つのモジュールを修正しないといけない!となっても、他のモジュールに与える影響が小さいです。) - MVCモデルを共通概念として、コードを共有することができる。
(他の人が書いたコードでも、Model、View、Controllerのモジュールに分かれていたら、どこで何をしているかだいたい想像がつきますよね。) - テストコードが書きやすくなる。
なお、この記事で取り上げる実装はあくまで一例です。もし余裕があれば、書いてあることを鵜呑みにするのではなく、「もっと良いコードにするにはどうすれば良いだろう?」のような観点でも見てみましょう。
※この記事では、基本的な文法やライブラリの使用方法については触れません。これらについては、以下の記事を参考にどうぞ。

環境
- Python3.10.4
Windows10で動作を確認しましたが、他のOSでも問題ないかと思います。
リバーシの設計
はじめに設計の話に入っていきます!最初は難しく感じるかもしれませんが、「ふーんそんなものか」と思ってもらえればOKです。
まず、リバーシを実装するために必要な機能を考えてみます。
- 盤面を表示する。
- 盤面のマスをクリックする。
- 挟まれたコマをひっくり返す。
- コマを置けるマスと置けないマスを区別する。
こんな感じでしょうか。今回は個人で開発するので、ここは思いつくままに書いて、後から必要なものを付け足していくのでも良いでしょう。
これらの機能を実装するために、必要なモジュールを考えます。今回は以下4つのモジュールを作っていきます。MVCの3つと、エントリポイント(実行時に最初に実行されるプログラムの箇所)となるmainですね。

ここで注意です。今回はMVCの3モジュール(+main)に分けましたが、必ずしもMVCをきれいに3つに分ける必要はありません。MVCモデルはあくまでソフトウェアアーキテクチャの一種ですので、実装や修正のしやすさやを考えて決めましょう。例えば、コントローラが1つではなく2つだったり、です。
では、各モジュールの役割について説明します。文章だけ読むと分かりにくいので、図を見ながら読み進めてみてください。
モデル(model.py)では、リバーシのロジックを扱います。「〜の盤面の状態で、このマスに〜(白または黒)のコマを置くと、盤面の状態は〜になる」といった処理を行います。盤面の情報は変数として持っておき、ゲームの最初に初期化します。その後は、コントローラが「このマスにこのコマを置いて!」と指示してくれるので、「置いたら盤面はこうなるよ!」という、盤面の状態を返すイメージです。
ビュー(view.py)では、ユーザ(リバーシで遊ぶ人)が操作するGUIを扱います。8×8の盤面を表示して、盤面のマスをクリックしたら「このマスが押されたよ!」とコントローラに伝えます。すると、コントローラは次の盤面の状態を知らせてくれます。
コントローラ(controller.py)は、ユーザの入力をビューから受け取り、モデルに渡します。また、モデルから処理結果を受け取り、ビューに渡します。言わば、ビューとモデルの橋渡し役ですね。ここで、「モデルも2次元で盤面を管理していればコントローラは存在意義が無いのでは?」と思うかもしれません。実は、コントローラがあることで、ビューはモデルの実装に依存しなくなるのです。例えば、今回はモデルで1次元配列を扱いますが、後々2進数で盤面を表現したモジュールを使いたくなるかもしれません。その場合にも、コントローラがあれば画面の表示とデータのやり取りを分離することができます。つまり、ビューはいじらずにコントローラのみ変更すれば良いということです。モデルの変更は画面の表示と本質的には関係がありません。ですので、ビューとモデルのインターフェイス差異を解決してくれるコントローラは大いに存在意義位があるのです。
mainはエントリポイントです。ビューを呼び出して、リバーシの画面を表示させます。ビューを直接呼び出しても良いのですが、エントリポイントがあるとプログラムがどこから始まるかが明確になるため、コードを読みやすくなります。
なお、この記事のコードを試したい場合、これらのモジュールは同じフォルダに配置するようにしてください。
モデル(Model)
モデルモジュールでは、以下のリバーシ処理を実装します。
- 盤面を初期化する。
- コマを置き、ひっくり返す。
ここで、盤面は以下のような、要素数100の1次元配列で扱うことにします。詳しくは触れませんが、1次元配列として扱うほうが、2次元配列として扱うよりもちょっとだけ実装が楽になるのです。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
| 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 |
| 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 |
| 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 |
| 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 |
それぞれのマスに書いてある数字は、要素のインデックスを表します。盤面左上のマスを11番目、盤面右下のマスを88番目とし、表1の一番外側の行と列は盤面の外を表すものとします。盤面の外のマスを用意しておくことで、実装がシンプルになります。用意しない場合は配列の外かどうかの判定が余計に入ってしまいます。
今回は、以下のように整数値とマスの状態を対応付けることにします。
- 空マス(EMPTY)は0
- 黒のコマがおかれているマス(BLACK)は1
- 白のコマがおかれているマス(WHITE)は2
- 外側のマス(WALL)は3
例えば、図2の盤面の状態は、
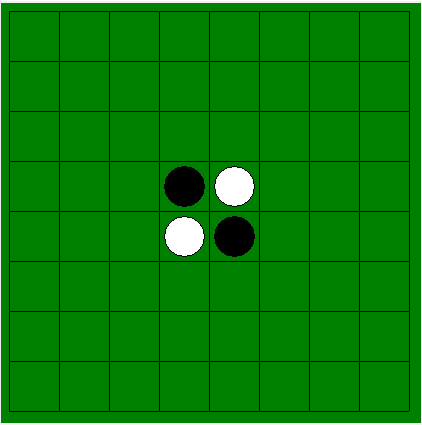
以下の配列に対応します。
[
3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 0, 0, 0, 1, 2, 0, 0, 0, 3,
3, 0, 0, 0, 2, 1, 0, 0, 0, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 3, 3, 3, 3, 3, 3, 3, 3, 3
]
図2における一番左、一番上を0番目とすると、左からx番目、上からy番目のマスは配列の10*(y + 1) + (x + 1)番目に対応します。
以上の考え方でコードを書くと、以下のようになります。
model.py
class ReversiModel:
# マスの状態を表す値
EMPTY = 0 # 空マス
BLACK = 1 # 黒のコマ
WHITE = 2 # 白のコマ
WALL = 3 # 壁
def __init__(self):
"""
初期化
"""
# 全てEMPTYで盤面を作成
self.board = [self.EMPTY] * 100
# BLACKとWHITEのコマを配置
self.board[44] = self.BLACK
self.board[55] = self.BLACK
self.board[54] = self.WHITE
self.board[45] = self.WHITE
# WALLを設定
for i in range(10):
self.board[i] = self.WALL
self.board[90 + i] = self.WALL
self.board[10 * i] = self.WALL
self.board[10 * i + 9] = self.WALL
def flip_list(self, i_board: int, top: int) -> list[int]:
"""
盤面のi_boardにtop(BLACK or WHITE)を置いたときに、
ひっくり返されるマスのリストを返す
"""
# 空マス以外なら空のリストを返す
if self.board[i_board] != self.EMPTY:
return []
# 相手のコマ
enemy = self.BLACK if top == self.WHITE else self.WHITE
# ひっくり返されるマスのリスト
tops = []
# 方向パラメータ
UP, DOWN, LEFT, RIGHT = -10, 10, -1, 1
# 8方向を走査
for v in (RIGHT, RIGHT + UP, UP, LEFT + UP, LEFT, LEFT + DOWN, DOWN, RIGHT + DOWN):
# ひっくり返す候補
temp = []
# i_boardとの差
delta = v
while self.board[i_board + delta] == enemy:
# 敵のコマならひっくり返す候補に加える
temp.append(i_board + delta)
delta += v
if self.board[i_board + delta] == top:
tops += temp
return tops
def put(self, i_board: int, top: int) -> bool:
"""
盤面のi_boardにtop(BLACK or WHITE)を置き、
同じ色ではさんでいるマスをひっくり返す
ひっくり返したらTrueを返す
"""
tops = self.flip_list(i_board, top)
if tops:
self.board[i_board] = top
for i in tops:
self.board[i] = top
return True
return False
なお、今回は各モジュールをクラスとして作成します。関数にしても良いのですが、ここはお好みですね。
さて、Modelで扱う処理は「盤面の初期化」と「コマを置き、ひっくり返す」でした。それぞれ、__init__()メソッドとput()メソッドが対応しています。put()は成功するとTrueを返し、置けない場所を指定するとFalseを返します。
このモジュールの核となるのが、flip_list()メソッドです。これは、指定のマスに指定のコマを置いたときに、コマがひっくり返るマスの座標リストを返します。
例えば
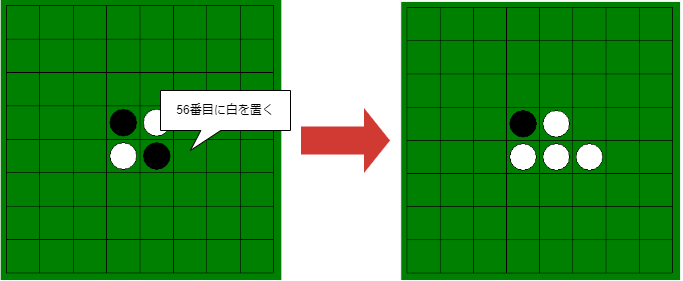
という操作をした場合、flip_list()はリスト[55]を返します。これは、「56番目のマスに白のコマを置くと、55番目のマス1つがひっくり返る」ことを示します。
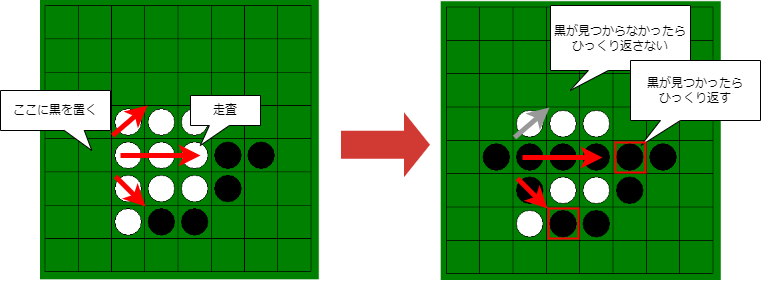
flip_list()の実装の考え方は以下の通りです。
- 指定マスから8方向に走査する。
- それぞれの方向について
- 置くコマと違う色のコマ(置くコマが黒なら白、白なら黒)がある限り走査を続ける。
- 置くコマと同じ色のコマがあったら、それまで走査したマスの座標をひっくり返すマスとする。
以下にモデルモジュールの使用例を示します。見やすいように出力を加工しています。
>>> import model
>>> m = model.ReversiModel()
>>> m.board
[
3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 0, 0, 0, 1, 2, 0, 0, 0, 3,
3, 0, 0, 0, 2, 1, 0, 0, 0, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 3, 3, 3, 3, 3, 3, 3, 3, 3
]
>>> m.put(56, m.WHITE)
True
>>> m.board
[
3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 0, 0, 0, 1, 2, 0, 0, 0, 3,
3, 0, 0, 0, 2, 2, 2, 0, 0, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 0, 0, 0, 0, 0, 0, 0, 0, 3,
3, 3, 3, 3, 3, 3, 3, 3, 3, 3
]これは、図3の操作を表しています。ReversiModelクラスのインスタンス生成時に盤面を初期化します。put()メソッドでボードの56番目(上から5番目、左から6番目)のマスに白を置いています。白を置いた後のm.boardの出力で、赤い箇所が変化した部分です。白(2)が置かれ、黒のコマ(1)が白(2)にひっくり返ったということですね。
コントローラ(Controller)
コントローラモジュールでは、ビューから受け取る情報をモデルに受け流します。今回、ビューでは盤面を2次元座標で扱いたいとします。モデルでは盤面を1次元座標で扱っていたため、ビューから使うためには、2次元座標を1次元座標に変換してあげる必要があります。
具体的には、ビューで扱う盤面では座標を表2の通り指定したいとします。左からx番目(0始まり)、上からy番目(0始まり)のマスを(x,y)と表します。例えば、モデルでの27番目のマスは、ビューでは(6, 1)として指定することになります。なお、こちらでは盤面の外は扱わないため、マスの数は8×8の64です。
| (0,0) | (1,0) | (2,0) | (3,0) | (4,0) | (5,0) | (6,0) | (7,0) |
| (0,1) | (1,1) | (2,1) | (3,1) | (4,1) | (5,1) | (6,1) | (7,1) |
| (0,2) | (1,2) | (2,2) | (3,2) | (4,2) | (5,2) | (6,2) | (7,2) |
| (0,3) | (1,3) | (2,3) | (3,3) | (4,3) | (5,3) | (6,3) | (7,3) |
| (0,4) | (1,4) | (2,4) | (3,4) | (4,4) | (5,4) | (6,4) | (7,4) |
| (0,5) | (1,5) | (2,5) | (3,5) | (4,5) | (5,5) | (6,5) | (7,5) |
| (0,6) | (1,6) | (2,6) | (3,6) | (4,6) | (5,6) | (6,6) | (7,6) |
| (0,7) | (1,7) | (2,7) | (3,7) | (4,7) | (5,7) | (6,7) | (7,7) |
図1からも分かりますが、今回のコントローラの主な仕事は、座標を2次元と1次元相互に変換してあげることですね。
- 画面から受け取った2次元座標を1次元座標に変換し、モデルに渡す。
- モデルからの結果盤面を1次元座標から2次元座標に変換し、ビューに渡す。
- 白と黒、どちらのターンであるかを管理する。
3つ目のターン管理はコントローラで行うべきか悩みどころですが、今回は
- ビューでターン管理をしたくなかった。
- モデルは純粋にリバーシロジックのみを扱いたかった。
という理由でコントローラで行うことにしました。「モデルではロジックだけでなく、ゲーム全体を管理したい」ということであれば、モデルでターン管理するのもありだと思います。
これをコーディングすると、以下のようになります。
controller.py
from model import ReversiModel
class ReversiController:
EMPTY = ReversiModel.EMPTY
BLACK = ReversiModel.BLACK
WHITE = ReversiModel.WHITE
def __init__(self):
"""
初期化
"""
self.rm = ReversiModel()
self.turn = self.WHITE
def put(self, x: int, y: int) -> None:
"""
(x, y)にコマを置く
"""
x += 1
y += 1
if self.rm.put(10 * y + x, self.turn):
self.turn = self.WHITE if self.turn == self.BLACK else self.BLACK
@property
def board(self) -> tuple[tuple[int]]:
"""
盤面を返す
盤面には[x][y]でアクセスする
"""
bd = [self.rm.board[10 * i + 1:10 * i + 9] for i in range(1, 9)]
return tuple(zip(*bd))コントローラは以下のように使うことができます。これも図3と同じ操作をしています。なお、c.boardは[x][y]でアクセスできるようにしているため、((行,行,…)ではなく)(列,列,…)の形になっています。モデルのときの出力とは反転した形となっているので、注意してください。こちらも見やすいように出力を加工しています。
>>> import controller
>>> c = controller.ReversiController()
>>> c.board
(
(0, 0, 0, 0, 0, 0, 0, 0),
(0, 0, 0, 0, 0, 0, 0, 0),
(0, 0, 0, 0, 0, 0, 0, 0),
(0, 0, 0, 1, 2, 0, 0, 0),
(0, 0, 0, 2, 1, 0, 0, 0),
(0, 0, 0, 0, 0, 0, 0, 0),
(0, 0, 0, 0, 0, 0, 0, 0),
(0, 0, 0, 0, 0, 0, 0, 0)
)
>>> c.put(5, 4)
>>> c.board
(
(0, 0, 0, 0, 0, 0, 0, 0),
(0, 0, 0, 0, 0, 0, 0, 0),
(0, 0, 0, 0, 0, 0, 0, 0),
(0, 0, 0, 1, 2, 0, 0, 0),
(0, 0, 0, 2, 2, 0, 0, 0),
(0, 0, 0, 0, 2, 0, 0, 0),
(0, 0, 0, 0, 0, 0, 0, 0),
(0, 0, 0, 0, 0, 0, 0, 0)
)boardプロパティで盤面を参照することが出来ます。また、put()メソッドで座標を指定してコマを置いています。
ビュー(View)
ビューでは画面表示とユーザからの入力受付を扱います。クリックされたマスの座標をコントローラに渡し、結果に応じて画面を描画しなおします。
リバーシの盤面を描画するためには、まず盤面やマスの長さを決めてあげる必要があります。今回は各パラメータの名前を、図5の通り定義することにしました。
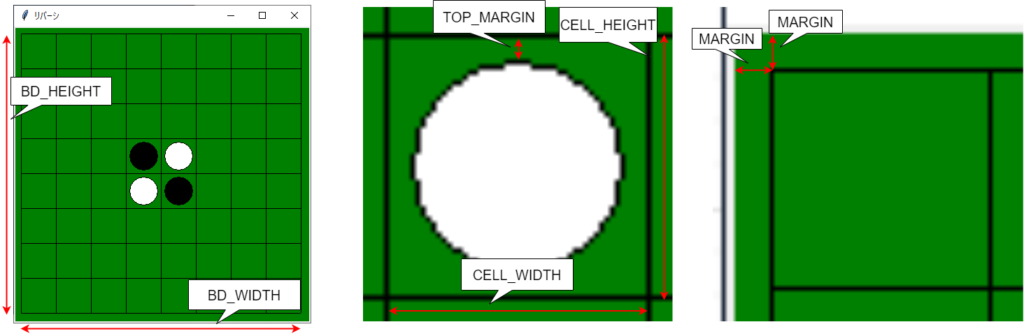
ではビューモジュールのコーディングに入っていきましょう。今回は、盤面の描画には標準モジュールのtkinterを使用しました。
view.py
import tkinter as tk
from controller import ReversiController
class ReversiView:
EMPTY = ReversiController.EMPTY
BLACK = ReversiController.BLACK
WHITE = ReversiController.WHITE
CELL_WIDTH = 50
CELL_HEIGHT = 50
TOP_MARGIN = 5
MARGIN = 10
BD_WIDTH = CELL_WIDTH * 8 + MARGIN * 2
BD_HEIGHT = CELL_HEIGHT * 8 + MARGIN * 2
def __init__(self):
"""
初期化
"""
# 盤面を描画
self.root = tk.Tk()
self.root.title("リバーシ")
self.canvas = tk.Canvas(
self.root,
bg = "green",
width = self.BD_WIDTH,
height = self.BD_HEIGHT
)
# コントローラを作成
self.controller = ReversiController()
# 描画
self.flash()
# イベントを設定
self.canvas.bind("<ButtonPress>", self.click)
# キャンバスを配置
self.canvas.pack()
def click(self, event) -> None:
"""
盤面をクリックしたときの処理
"""
# クリックされたマスの座標
x = (event.x - self.MARGIN) // self.CELL_WIDTH
y = (event.y - self.MARGIN) // self.CELL_HEIGHT
self.controller.put(x, y)
self.flash()
def draw_top(self, x: int, y: int, top: int) -> None:
"""
canvasにコマを描画する
"""
# コマの色
top_color = "white" if top == self.WHITE else "black"
# 円を描画
self.canvas.create_oval(
x * self.CELL_WIDTH + self.MARGIN + self.TOP_MARGIN,
y * self.CELL_HEIGHT + self.MARGIN + self.TOP_MARGIN,
(x + 1) * self.CELL_WIDTH + self.MARGIN - self.TOP_MARGIN,
(y + 1) * self.CELL_HEIGHT + self.MARGIN - self.TOP_MARGIN,
fill=top_color
)
def flash(self) -> None:
"""
盤面の状態をキャンバスに描画する
"""
# 画面をクリアする
self.canvas.delete("all")
# 線を描画
for y in range(self.MARGIN, self.MARGIN + self.CELL_WIDTH * 8 + 1, self.CELL_WIDTH):
self.canvas.create_line(self.MARGIN, y, self.MARGIN + self.CELL_WIDTH * 8, y)
for x in range(self.MARGIN, self.MARGIN + self.CELL_HEIGHT * 8 + 1, self.CELL_HEIGHT):
self.canvas.create_line(x, self.MARGIN, x, self.MARGIN + self.CELL_HEIGHT * 8)
for x in range(8):
for y in range(8):
match self.controller.board[x][y]:
case ReversiController.BLACK:
self.draw_top(x, y, ReversiController.BLACK)
case ReversiController.WHITE:
self.draw_top(x, y, ReversiController.WHITE)
def run(self) -> None:
"""
実行
"""
self.root.mainloop()
クラス変数定義部分で、マスの状態を表すパラメータと、図5の各パラメータの値を決めています。白または黒のコマが置かれたマスはBLACK,WHITE、何も置かれていないマスはEMPTYとしています。
__init__()メソッドでは、画面の初期化とコントローラの初期化を行っています。盤面の状態や、今はどちらのターンであるかなどはコントローラ(self.controller)(とモデルモジュール)で管理してくれるので、ビューからはクリックされた座標をコントローラに渡せば、盤面の状態を更新することができます。このように、画面の描画を行うビューモジュールにとって、盤面の更新処理は本質的ではなく、あまり意識したくない部分です。これを、「ビューにとって盤面の更新処理は無関係な下位問題[1]である」といい、処理を切り分けることで読みやすいコードとなります。
実際にクリックした座標をコントローラに渡しているのがclick()メソッドです。座標をx,yとして計算し、controllerのput()メソッドに渡しています。そのあと盤面がどうなるかについては、controllerに任せることができるということですね。
draw_top()メソッドでは、指定された座標にコマを描画します。描画の際には、図5の通りマスの端とコマの間に隙間(TOP_MARGIN)を作るようにしています。canvasのcreate_oval()メソッドで、範囲と色を指定して円を描画しています。この円をコマとしています。
flash()メソッドでは、最初に盤面をクリアし、次に線を描画し、最後にコントローラから盤面の状態(self.controller.board)を参照し、それを描画しています。コマを描画する際は、盤面のうち黒か白が置かれている箇所に、draw_top()メソッドを使って描画しています。
run()メソッドではself.rootオブジェクトのmainloop()メソッドにて、__init__()で初期化したself.rootオブジェクトを使い、無限ループ表示します。これがGUIとしての表示となるわけです。
エントリポイント
最後に、エントリポイントとなるmainモジュールを作成します。といっても、ビューモジュールを起動するだけです。
main.py
from view import ReversiView
if __name__ == "__main__":
view = ReversiView()
view.run()
ここまで実装すれば、モジュールのあるフォルダで、以下のようにリバーシゲームを起動することができます。
python main.py
# または
# python3 main.pyMVCモデルのメリット
さて、ここまで4つのモジュールを作成しましたが、こんなことをしなくても1モジュールですべて実装することもできます。なぜこんなことをするかと言えば、冒頭で述べたようなメリットがあるからなのですが、モジュール変更の観点でもう少し具体的に考えてみましょう。
「今のままだとゲーム画面が寂しいので、もっとリッチな描画にしたい。」
と思ったとします。今回の設計なら、図6のようにviewモジュールを新しいniceviewモジュールに取り換えることで対応できます。

これがモジュール分割をしない場合どうなるかというと、(大抵は)画面描画とリバーシロジックが混在したコードになるので、画面以外の処理も意識しながら修正する必要がでてきます。ロジック部分で使っている変数を画面描画部分の処理で意図せず書き換えてしまっていた、なんてことが発生するかもしれません。
ちなみに、「クラスはただ一つだけの責任を持つように設計し、カプセル化すべきである」という考え方を単一責任の原則(The Single Responsibility Principle)[2]と言います。一つのモジュールに画面描画、リバーシロジックといった複数の責任を持たせるのは(多くの場合)望ましくありません。
課題
今回作ったリバーシゲームは、以下の機能に対応していません。練習として実装してみましょう。
- パス
置けるマスがなくなってもパスできないため、そこでゲーム終了となってしまいます。 - 勝敗表示
ゲームが終わっても勝敗が表示されないため、コマを数えないと勝敗が分かりません。 - 置けるマスの表示
次のプレイヤーが、どこのマスにコマを置けるかを表示すると親切ですね。
まとめ
この記事では、リバーシゲームの実装と、MVCモデルについて説明しました。
MVCモデルとはソフトウェアアーキテクチャの一種で、今回はそれに則ってリバーシゲームを作成しました。MVCモデルに則ることで、より分かりやすく、保守性の高いコードを作成することができます。
モデルではリバーシロジックを、ビューでは盤面の表示と入力の受け付けを、コントローラはビューとモデル間のデータの橋渡しを行います。このように役割分担することで、後々のモジュール変更などに柔軟に対応することが可能となります。
あとがき
リバーシのロジックは、初めて書く場合は少し難しいです。昔、自分で考えたコードがきちんとリバーシのルール通りに動いているのを見て「おお…!」と感動したのを覚えています。これが自力で書けるようになれば、一通りの基礎的なプログラミング能力があると言えるでしょう。(基礎は大事です!)
モジュール分割するべきかどうかは場合によりますが、ある程度大きい、もしくは大きくなりそうなコードを書くときは、機能ごとにモジュールを分けた方が良いです。
ただ、あくまで分かりやすいコードを書くことが目的なので、たとえGUIを扱うソフトウェアだとしても、あまりMVCというモデルにこだわる必要はありません。無理やりMVCの形にあてはめて分かりにくくなったら本末転倒です。臨機応変に適切な設計ができるようになりましょう。(私もできるようになりたいです。)
参考文献
[1]Dustin Boswell,Trevor Foucher (2011). The Art of Readable Code. O’Reilly Media.(ダスティン・ボズウェル,トレバー・フーシェ(著) 角 征典(訳)(2012). リーダブルコード―より良いコードを書くためのシンプルで実践的なテクニック オライリー・ジャパン)
[2]Robert C. Martin(2005).The Principles of OOD.http://www.butunclebob.com/ArticleS.UncleBob.PrinciplesOfOod, (参照 2023-02-18)

